Protective puts are a foundational options technique for limiting downside risk while maintaining exposure to potential gains. The strategy pairs a long underlying position with a long put option on the same asset. The put establishes a floor under the portfolio value for a specified period, at the cost of the option premium. In contrast to reactive tools such as stop orders, protective puts provide contractual protection against adverse price moves, including gaps. This article explains the core logic, mechanics, and risk management considerations of protective puts, and shows how the approach can be integrated into structured, repeatable trading systems without recommending specific trades or price levels.
Definition and Core Mechanics
A protective put is created by holding the underlying asset and simultaneously purchasing a put option on that asset. The put provides the right, but not the obligation, to sell the underlying at the put’s strike price during the life of the contract. If the asset price declines below the strike, the intrinsic value of the put offsets part or all of the underlying losses. If the asset price rises, the put can expire worthless while the underlying gains remain intact, net of the premium paid.
The resulting position is sometimes described using put-call parity. Conceptually, a long underlying position plus a long put is economically similar to owning a long call plus a risk-free bond whose value equals the present value of the strike. This identity highlights the insurance-like nature of the put and clarifies that protection is not free. The premium embeds the market’s assessment of expected volatility, skew, interest rates, and dividends over the option’s life.
Payoff Structure
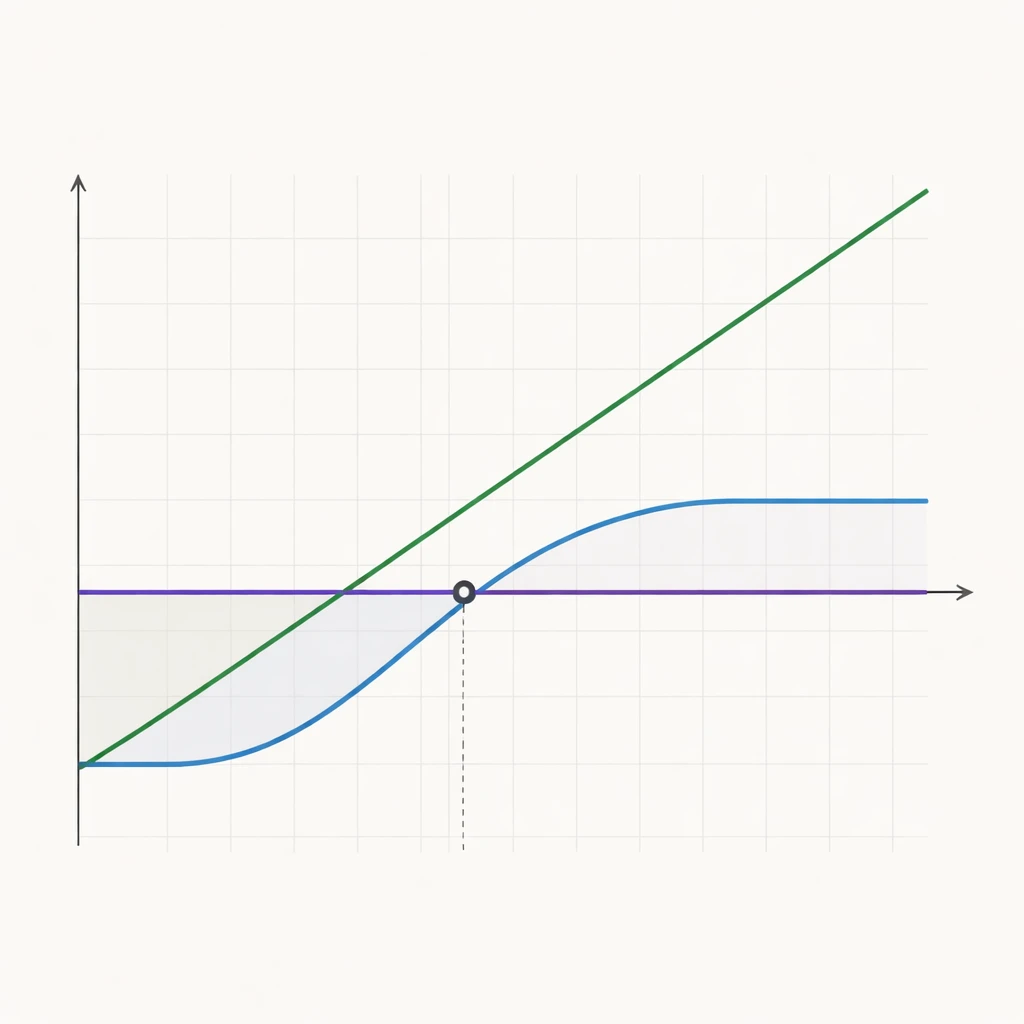
The protective put payoff combines linear upside from the underlying with a non-linear floor created by the put. The floor is located near the put strike, minus the option premium. Although the strike defines the level at which the option begins to offset losses, the net result for the combined position includes the cost of the put. The premium is paid upfront, reduces expected return by that amount, and increases the certainty of the worst-case outcome for the covered period.
Visually, the payoff line resembles an equity curve that rises with the underlying price but flattens below the strike, reflecting losses limited to a bounded amount for the protection window. This bounded downside is the primary reason investors use protective puts in settings where gaps or sharp adverse moves are possible.
Why Use Protective Puts
Protective puts serve several purposes:
- Limiting downside during volatile regimes while preserving upside participation.
- Hedging specific event risk when potential discontinuities are plausible.
- Reducing the depth of drawdowns to support risk budgeting and portfolio constraints.
- Providing psychological and process discipline through pre-defined loss containment.
The strategy is not intended to eliminate risk. It transforms the distribution of outcomes by replacing unbounded downside with a known worst-case range for a defined time, while transferring some expected return to option sellers through the premium.
Position Construction and Choice Variables
Constructing a protective put involves several design choices that can be systematized:
Strike Selection
Strike selection determines the location of the protection floor and the cost of the hedge. A higher strike places the floor closer to the current price, which typically costs more because the put is more likely to finish in the money. A lower strike reduces cost but allows a larger loss before protection becomes effective. System designers often express strike selection as a function of the current price or of measures such as average true range, recent volatility percentiles, or drawdown tolerances. The key is to align the strike with a pre-defined risk budget rather than a discretionary view.
Expiration Selection
Expiration controls the protection horizon and the frequency of hedge renewal. Short-dated puts cost less in absolute premium but require frequent rolling and expose the position to timing risk between rolls. Longer-dated puts offer sustained protection at higher upfront cost and a different sensitivity profile to volatility. Choice of tenor is often linked to the expected duration of risk, portfolio turnover, and administrative capacity to monitor and roll options on a schedule.
Underlying Coverage and Basis Risk
Protective puts can be purchased on the exact asset held or on a correlated proxy such as an index. Hedging a diversified equity portfolio with index puts introduces basis risk, the possibility that the portfolio and the index diverge. A systematic approach can quantify the hedge ratio using beta estimates, sector weights, or factor exposures, while recognizing that these relationships are imperfect and time varying.
Greeks and Sensitivity Profile
The combined position exhibits a set of risk sensitivities that change as price and time evolve.
- Delta: The long underlying has positive delta. The long put has negative delta, which becomes stronger as price falls and weaker as price rises. Near and below the strike, the net delta is reduced, limiting downside exposure. Far above the strike, the net delta approaches that of the unhedged underlying.
- Gamma: The long put contributes positive gamma, which increases as the price approaches the strike from above. Positive gamma helps the position respond more favorably to sudden moves by increasing the hedge effect when losses accelerate.
- Theta: The long put has negative theta. Time decay erodes option value when protection is not needed. This decay is the explicit cost of carrying insurance.
- Vega: The long put benefits from increases in implied volatility. In market stress, implied volatility often rises, which can enhance the value of the hedge precisely when it is needed.
Understanding these sensitivities allows a system designer to anticipate how the hedge behaves across paths, not just at expiration. It also clarifies why realized protection can differ from static payoff diagrams, especially when rolling is part of the plan.
Cost, Budgeting, and Opportunity Cost
Every protective put consumes premium that could have been invested elsewhere. Effective use therefore begins with an explicit hedge budget. A budget can be expressed as a percentage of portfolio value allocated to protection over time. The budget should be tied to the objective of reducing drawdowns or tail risk within tolerances that address both financial and organizational constraints.
Cost varies across volatility regimes. Implied volatility tends to rise when markets become unsettled, which makes protection more expensive precisely when demand increases. A systematic approach can adapt hedge intensity to regime estimates, without relying on discretionary timing. Some programs scale strike or tenor as a function of implied volatility percentiles. Others maintain a steady schedule to reduce timing risk, accepting that cost will be higher in stressed periods.
Opportunity cost arises because premium paid reduces expected return compared to an unhedged position. Whether the trade-off is acceptable depends on the value placed on drawdown mitigation, smoother return paths, or compliance with risk limits. The answer is not universal and should be grounded in policy rather than short-term outcomes.
Timing, Events, and Regimes
Protective puts can be used continuously or episodically. Continuous hedging seeks to maintain a persistent floor and accepts ongoing premium expense. Episodic hedging targets periods surrounding known events or when volatility regimes appear elevated based on pre-defined indicators. Both approaches can be made repeatable by codifying triggers and rebalancing rules that do not depend on forecasting price movement.
Event-focused protection is sensitive to the possibility that markets move prior to the event, which can increase option cost. Continuous programs face the challenge of paying for protection when it is not needed. Hybrid designs balance these issues by setting a base level of protection with the capacity to scale within a budget.
Rolling and Lifecycle Management
A protective put program requires rules for monitoring and rolling:
- Time-based rolls replace options on a calendar schedule to maintain a consistent horizon.
- Delta or moneyness-based rolls adjust the hedge when the underlying has moved significantly, to keep the floor aligned with the risk budget.
- Volatility-aware rolls respond to changes in implied volatility, which affect the cost and effectiveness of replacement options.
Roll rules should be simple, measurable, and aligned with the constraints of trading frequency and liquidity. For long American-style puts, there is no assignment risk from the long side. Early exercise decisions can arise if the put is deep in the money and time value is minimal, but in many cases selling the option preserves remaining extrinsic value more effectively than exercising. Operationally, liquidity and transaction costs matter, especially when rolling frequently or when hedging less liquid assets.
Integration into Structured, Repeatable Systems
Protective puts fit naturally into systematic portfolio construction because they convert an open-ended downside into a policy-defined floor. Integration often follows a sequence:
- Set risk objectives: define acceptable drawdown, volatility targets, and tail risk thresholds in advance.
- Translate objectives to design choices: map drawdown targets to strike selection, tenor, and hedge coverage ratio.
- Allocate a premium budget: specify annualized limits to hedge spending as a percentage of assets.
- Codify rebalancing: choose roll schedules and adjustment triggers measurable ex ante.
- Define performance metrics: evaluate whether the hedge achieves the intended risk outcomes net of cost.
These steps transform protective puts from ad hoc trades into a disciplined component of a broader risk framework. Consistency helps isolate whether the program meets its purpose rather than being judged by short-term payoff variability.
Measuring Effectiveness
Evaluation should focus on risk-adjusted outcomes, not isolated wins or losses on the options. Useful metrics include:
- Maximum drawdown reduction relative to an unhedged baseline.
- Volatility and downside deviation changes, including Sortino ratio effects.
- Tail risk measures such as expected shortfall.
- Skewness and kurtosis of returns, which capture distribution shape changes.
- Hedge cost as a predictable share of returns, compared to the value of risk reduction.
Backtests should include transaction costs, realistic liquidity assumptions, and slippage. Stress tests can examine crash scenarios, sudden volatility spikes, and regime changes. Case studies that evaluate different strikes and tenors across regimes provide insight into robustness.
Comparison with Alternative Risk Controls
Protective puts are one element in a spectrum of risk controls.
Stop orders are reactive and can trigger at unfavorable prices during gaps. They do not define the worst-case outcome ahead of time. Protective puts specify a floor within the option’s life, at the cost of premium. Trailing stops may reduce the distance to exit as prices rise, but they remain exposed to gap risk. Structural diversification and position sizing attack risk at the portfolio level. A protective put can complement these methods by specifying a loss boundary for a particular exposure or for a portfolio proxy.
Dynamic hedging with futures or delta-hedged options can simulate protection but introduces path dependency and operational complexity. Protective puts are path independent at expiration, which simplifies outcome analysis, though rolling introduces its own path effects.
Variations and Extensions
Several related structures reduce premium outlay or tailor protection to specific objectives:
- Collars: long underlying, long put, and short call. The call premium helps finance the put but caps upside beyond the call strike. Collars translate the protective put into a bounded return range consistent with a defined policy.
- Put spreads: long a higher strike put and short a lower strike put. This reduces premium but allows losses between the two strikes, with full protection only below the lower strike.
- Index overlays: hedging a portfolio with index puts. This introduces basis risk but can be more liquid and operationally efficient.
- Synthetic perspective: long underlying plus long put is economically related to a long call plus cash via put-call parity. This helps clarify the cost of protection and the role of interest rates and dividends.
Event Risk and Earnings-Type Scenarios
When outcomes are particularly uncertain over a short window, the convexity of puts can be valuable. The long put benefits from abrupt declines that often coincide with volatility spikes. However, event windows can also inflate implied volatility, raising the cost of protection. A rule-based approach might specify conditions under which protection is increased, held steady, or reduced, guided by a pre-set premium budget and risk limits rather than discretionary predictions.
Liquidity, Market Microstructure, and Execution
Execution quality influences realized outcomes. Wider bid-ask spreads and thin depth increase the effective cost of the hedge. System designs often prioritize liquid underlyings and option strikes with active order books. Time-of-day effects, coordination with roll schedules, and the use of limit orders can be codified to improve consistency. Slippage assumptions should be conservative in backtests to avoid overstating effectiveness.
Regulatory and Accounting Considerations
In some jurisdictions, the classification of hedges, treatment of option premiums, and tax implications differ by structure and intent. Portfolio managers may need to align documentation and reporting with hedge accounting standards or internal policy. Because rules vary and can change, systems should be flexible enough to accommodate policy constraints without altering the core logic of the hedge.
High-Level Example
Consider an investor with a concentrated equity position who aims to limit potential losses over the next quarter while retaining upside if the market advances. The investor maintains the equity position and buys a put that expires near the end of the quarter. The strike is selected to align with the investor’s maximum drawdown tolerance for that period and a predefined hedge budget. If the equity price declines significantly during the quarter, the put increases in value, absorbing a portion of the loss so that the portfolio value remains within the targeted loss boundary. If the equity price appreciates, the put may expire without value, and the investor realizes the equity gains reduced by the cost of the hedge. Throughout the period, the investor follows a documented rule for whether and when to roll the put, such as on a fixed date schedule, to maintain consistent protection into the next quarter.
This example avoids precise price levels or signals, yet it illustrates the structured nature of the approach. The protective put turns a vague aspiration to limit losses into a repeatable process with measurable parameters: strike proximity, tenor, budget, and roll protocol.
Common Pitfalls and Risk Management
Several practical issues arise when implementing protective puts:
- Underestimating cost: Premium outlay can accumulate during calm markets, which may tempt a shift away from the hedge just before it would have been most useful. A clear budget and governance process helps maintain discipline.
- Mismatched horizons: Selecting expirations that do not align with the period of risk can create gaps in protection if adverse moves occur after the option expires.
- Basis risk: Hedging a portfolio with index puts may not track well during idiosyncratic moves in specific holdings.
- Liquidity and execution: Infrequently traded options can impair rolling and inflate costs.
- Overfitting designs: Excessively optimized strike-tenor combinations in backtests may not hold out of sample. Simpler, robust rules are usually more durable.
Risk management starts with clarity about objectives. Protective puts work best when their role is carefully defined, such as limiting drawdowns to a specified range over a known horizon, and when the cost is treated as a known expenditure rather than a speculative bet.
Protective Puts in Portfolio Context
At the portfolio level, protective puts can be applied to single names, sectors, or broad indices. They can protect strategic holdings that are difficult to reduce for tax or mandate reasons. They also serve as a complement to position sizing, diversification, and factor balancing. When combined with policy constraints, protective puts help ensure that exposures remain within predefined risk envelopes, especially when markets become turbulent.
From an operational perspective, program governance matters. Documentation should specify the purpose of the hedge, eligible instruments, constraints on tenor and strike, and escalation procedures if costs exceed budget. Clear governance reduces reliance on judgment calls made under stress, which can be inconsistent and reactive.
Analytical Framework and Backtesting Considerations
A structured analysis of protective puts typically follows these steps:
- Baseline definition: establish the unhedged portfolio or exposure to serve as a benchmark.
- Rule set: codify strike, tenor, coverage ratio, roll schedule, and any regime-based adjustments.
- Cost modeling: include option premiums, transaction costs, and conservative slippage. Capture the term structure and skew of implied volatility when possible.
- Path dependency: simulate realistic price paths and include scenarios with gaps and volatility clustering to assess behavior beyond average conditions.
- Evaluation: quantify drawdown reduction, volatility changes, tail measures, and the premium-to-benefit trade-off.
Interpretation should emphasize whether the program meets risk objectives consistently, not whether it outperforms the unhedged position in every period. The value of protection is conditional, and the goal is to align outcomes with policy-defined tolerances.
When Protective Puts May Be Less Suitable
There are circumstances where the fit may be weaker. If the primary objective is to maximize long-run expected return without constraints on drawdown, protection costs may be difficult to justify. If the investment horizon far exceeds the hedge horizon, repeatedly rolling puts can create persistent drag. For highly diversified exposures with low idiosyncratic risk, portfolio-level techniques like rebalancing and sizing may address much of the risk at lower cost, with protective puts reserved for specific tail concerns.
Putting the Components Together
Protective puts convert uncertain downside into a defined range for a defined time. The approach becomes most effective when embedded within a rules-based framework that aligns strike, tenor, budget, and rolling with explicit risk objectives. The success of such a program depends less on timing the market and more on process quality, governance, and consistency. When evaluated through the lens of distribution shaping, protective puts are a tool for engineering outcomes that respect constraints on loss while preserving participation in favorable moves.
Key Takeaways
- A protective put combines a long underlying position with a long put to set a downside floor for a defined period, at the cost of premium.
- Strike and expiration choices translate risk objectives into a measurable hedge design that can be implemented systematically.
- The strategy alters the return distribution by limiting drawdowns and adding negative carry through option decay.
- Effectiveness depends on regime dynamics, liquidity, disciplined rolling, and alignment with a pre-set hedge budget.
- Protective puts integrate naturally into structured risk management frameworks and can complement diversification and position sizing without relying on forecasts.